比赛中，轮式机器人的行走策略一般作匀速处理，但是由于惯性等因素，机器人往往不能准确到达目的地。本文对轮式机器人行走定位策略进行讨论研究，主要内容有：小车从速度0逐渐加速，一直加速到最大值，然后定速、减速、停车，如何处理最大速度？距离与速度存在函数关系，如何处理？
    我们让距离决定速度，可以绘画出它的“速度——距离关系图”（如图1），由小车行走距离决定程序的分段，当小车行走距离小于B时，不能达到最大速度；等于B时可以达到最大速度，但接着就减速运行；当距离大于B时，中段可以全速运行，然后留下减速距离使小车平稳减速到一个低速后到目标地C刹车。这种设计方式是符合平稳的机械运动规律的。
    当行走距离是A时，在行走了距离A′时就减速了，到A"时减到一个较低速，到A点时停车。
    当行走距离是B时，在行走到B′点时开始减速，到B"时减到了一个较低速，保持一个低速到B点停车。
    当行走距离是C时，在行走到C′点时，保持恒速运行到C′点然后开始减速，在到达C"点时保持一个低速到C点停车。

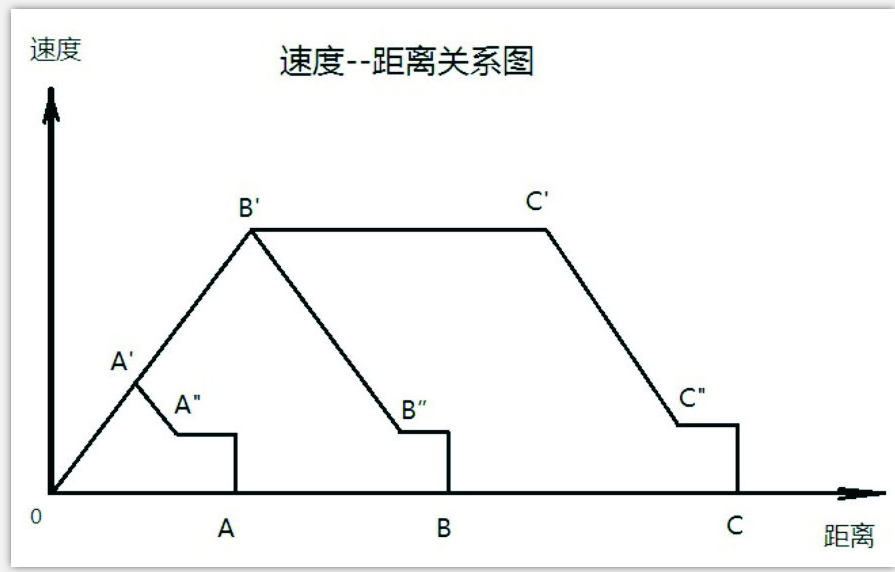
图1

    一、直线运动程序设计策略
    图2是这个直线运行子程序压缩后留出的参数设置图，它具有加速、减速、初始动力设置、距离/转角比系数设定、最大加速距离设定、减速距离设定、加速时间设定、减速时间设定以及两个马达的转速不对称微调这几项功能的参数设定。

图2

    小车搭建好，把程序输入后进行参数调试，一旦调试好，走直线的功能在主程序中只要输入需要行走的距离。例如走100毫米，调用子程序就能以很小的误差停到指定距离，不用为行走距离反复调试。
    如图3所示，加速段程序中马达为伺服马达，B马达是被测试对象（即设定距离对象），红色变量值是对马达进行设定的转动角度。马达函数是能控制其从-100到100步长是1的功能函数。
将B马达传感器清零，设定由B马达传感器决定加速过程的循环，之前将变量4清零（也可以设初值），当传给马达的能量小于96时（如果B、C马达对称不要微调，此处应该是99），给马达能量参数加1，马达B、C以此参数运行一小段时间（这里是千分之8秒），返回测试马达转角，小于设定值，继续马达能量加1循环，直到马达转角不小于设定值时，退出循环，完成加速过程。

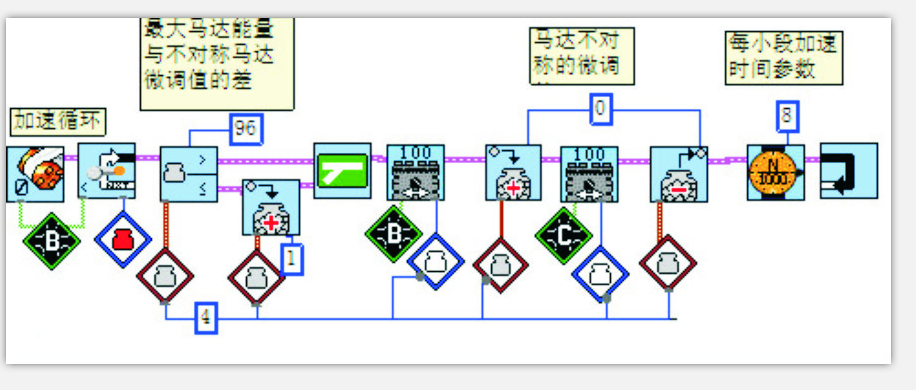
图3

    这一过程，马达能量随时间增大，速度增加的快慢由每小段加速时间决定。加速距离由设定的马达转角决定。此段程序一定会使小车走起来，哪怕是很小的距离（由伺服电机最小转角也就是分辨率决定）。因此，小车能以马达的最小分辨率角度的两倍行走。
    因此，我们看到这个小车会以每次毫米级量值移动。那么最小移动距离是多少呢？这要取决于轮子大小和伺服马达的分辨率。NXT的伺服马达是1度，因此，移动距离能产生2度的转动值，这个程序就能看到它使小车在移动，如果需要很高的精度进行小距离移动，则需要对小车进行角度与距离的整数倍关系进行选零件。
    当小车加速过程有偏向时，就要修改马达不对称参数，可以正或负，直到加速段不偏向为止，每次增加1进行调试，即对“马达不对称微调”处的参数修改。
    此段程序走完后，将由距离决定是恒速运行还是减速运行，当行走距离小于加、减速之和距离时，没有恒速段时间，进入减速运行。
    恒速部分只要对马达角度传感器循环检测就行，如果恒速行走有偏向时，可对恒速走偏进行微调，与加速时一样。
    如图4，减速段程序与加速段正好相反，只是有个最低能量值要设定，不然，小车还没有到达预定距离就停车了。减速时间短的话，减速很快，可能会打滑。

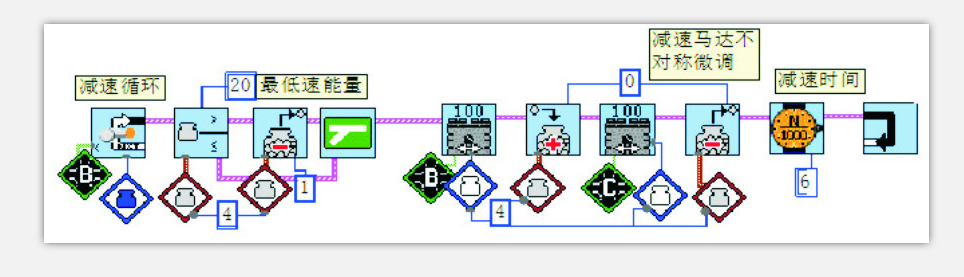
图4

    我们在实际的运行中观察到，有时我们并不需要最高速度运行，也就是说不要太快。我们需要低速长距离运行，那么我们可以使每小段的加速时间加长。此程序使小车低能量加速时间长，在不高的速度时就走完了加速时间或者说是加速距离，然后就以这个不高的速度恒速运行，因此，达到了低速长距离运行的目的。当然，这里需要把每小段的加速时间用参数传递进去。
    主程序送来的参数进行加减速距离设置处理，我们可以设定一个加、减速距离，如果主程序发来的数据小于等于“加、减速距离之和”这个参数时，就将参数分为两份，一份加速，一份减速，即加速、减速参数被赋值，恒速参数置零，恒速程序段便不执行。当主程序送来的参数大于这个参数时，设定加速、恒速距离与减速距离。
    我们把加速段马达能量初始值设为零，再设定轮子周长与转角关系，使得马达转角与行走距离成对应关系，因此，此程序适合于各种轮径的小车。例如：LEGO有一种轮子是直径81.6，周长是81.6*π≈256，轮子每转一圈走256毫米，360/256≈1.4，即每毫米要转1.4°，因此，从主程序来的以毫米为单位的距离值应该乘以1.4，Robolab2.9的这个变量是整形变量，因此，乘14再除以10就相当于乘1.4。
    另外，这个程序中的加速、减速距离的确定应该是可以作为运动学的题目来进行研究，以多少的加速距离可以完成加速到最大速度而不会打滑，这里要进行轮子与将要行走的地面的摩擦系数实验，马达的最大力矩是多少？以当前小车的质量能产生多大的加速度？当超过哪个范围将会产生行走误差？这些都有助于培养学生以科学为基础，以工程技术学来解决问题的理念。
    二、机器人转弯策略设计
    我们先来分析转弯过程中车轮的运行轨迹，当一个轮子不动、另一个轮子转动时，这就是以不动的轮子为中心、以轮距为半径进行的圆周运动，如图5所示：以C轮为中心、以两轮距长R为半径画圆，而以r为半径的轮子B走过的轨迹正是这个圆，因此，当小车转一圈时，我们计算大圆周长是小圆周长的多少倍，也就是说，小车转一周是要求B轮转多少圈，即周长的比值2πR/2πr，也就是R/r的值，换算到度就是再乘360。因此，小车转180度就是这个比值乘180，故我们在主程序中输入180，调用子程序后小车就会转180度。
（下转第14版）
（上接第15版）

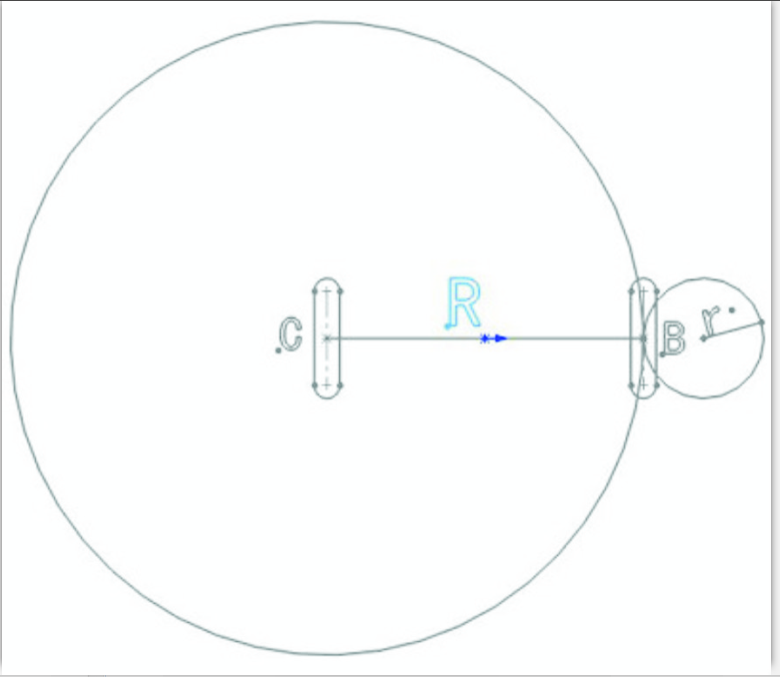
图5

    转弯程序与直线运动程序思想是一样的，有加速、减速过程，也有恒速过程，这里就不再重复描述。
    程序设计中，以两个驱动轮中心为圆心的旋转有以下几个要点：
    1.两个马达是反向转动，程序要处理这个正反转。
    2.加了正反向的不对称调整参数项，因为LEGO的电机同能量的正、反转速度是不一样的，所以同样的正反参数转的角度不一样。
    3.只用了B马达的传感器作为测试对象。其它与直线运动程序差别不大。旋转系数与前面说的原理是一样的，只是精度下降不少，没有一只轮子运动转弯的精度高。
    另外，运动中有一个减速快慢问题，即程序中设定的减速时间并不能适合所有情况，减速的快慢会直接影响定位精度，减速太快会打滑，减速时间长也是我们不希望的，它增加了完成任务的时间。因此，我们可以设置一个参数，由我们根据当时的情况来决定减速的快慢，即每小段减速时间可以临时给定。
    如图6，子程序头部把黄色变量的值加给3号变量，在这里的3号变量先给5的初值，然后加上黄色变量传来的值。在子程序里，减速时间用了3号变量的值，这里是千分之几秒的时间，即每变化一步用的时间。如果主程序中没有赋值黄色变量，那么子程序也有初始值保证原来的减速时间。
    以上的程序参数是某个特定小车的，不同的小车要进行参数修改，可以凭经验设置，也可以凭感觉设置，最好是根据以上方法去做有依据的设置。

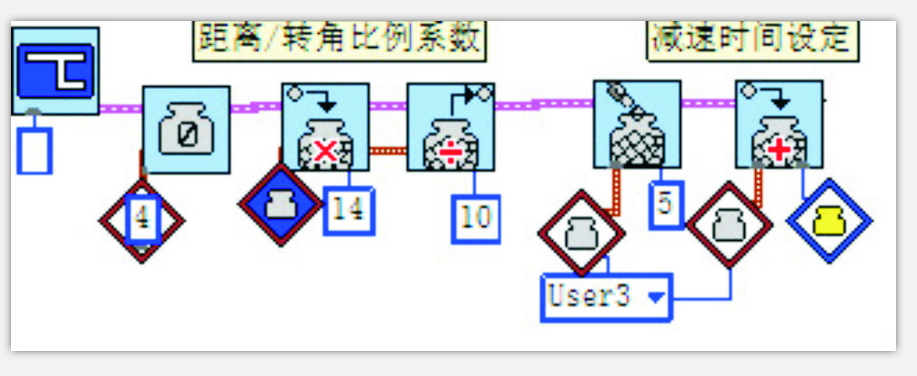
图6

    三、结束语
    设计机械运动的动作形式应该遵循运动学原理，我们在与中小学生讨论时，如果学生学习了牛顿定律，我们可以让学生去进行更深入的讨论；如果学生没有学习过牛顿定律，也可以用生活中的运动感觉或相关的现象来说明为什么要这样设计小车的运动程序，这对学生们更好地建立学习对象的思考模型很有好处。