令无数人为之着迷的π
在数学的漫长发展历程中,几乎没有哪个常数能像圆周率这样散发着经久不衰的魅力!
古希腊著名数学家阿基米德是第一个用科学的方法寻求圆周率数值的人。公元前3世纪,阿基米德画了一个内接于圆的正三角形,然后又画了一个外切于圆的正三角形。我们都知道,正多边形的边数越多,其周长也就越接近圆的周长,为此他不断增加多边形的边数。当正多边形的边数增加到96时,他得出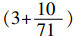 <π<
<π<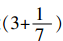 ,并计算出精确到小数点后两位的π值3.14,这是世界上首次计算出来的圆周率值。
,并计算出精确到小数点后两位的π值3.14,这是世界上首次计算出来的圆周率值。
到了公元3世纪,我国数学家刘徽在《九章算术》中创造性地提出“割圆术”,用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率。他最后计算出圆周率的近似值为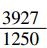 ,即3.1416,这个近似值在当时处于领先地位。
,即3.1416,这个近似值在当时处于领先地位。
刘徽之后两百多年,我国数学家祖冲之进一步钻研,从圆内接正六边形算起,一直算到圆内接正24567边形,得出圆周率应该在3.1415926和3.1415927之间,成为世界上首个把圆周率精确地推算到小数点后第七位的人,并将这一纪录保持了近千年!此外,祖冲之还提出了用“约率(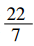 )”和“密率(
)”和“密率(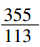 )”两个相当精确的分数来表示圆周率,闻名世界。
)”两个相当精确的分数来表示圆周率,闻名世界。
德国数学史家康托说:“历史上一个国家所算得的圆周率的准确程度,可以作为衡量这个国家当时数学发展水平的重要标志。”祖冲之的光辉成就恰恰反映了我国古代数学高度发展的水平,为纪念他,国际天文学家联合会把月球上的一座环形山命名为“祖冲之环形山”。
数学是一切科学的基础
时至今日,计算圆周率的新公式不断被发现,圆周率位数的世界纪录不断被打破……π的魅力也许就在于它的无穷无尽,正如人们对数学领域的钻研从未停歇。一些悬而未决的数学问题,历经千百年仍“顽固”地保守着自身的秘密,而每一个世纪难题的破解,或许意味着人类又找到一座隐匿着未知真理的巨大宝藏。
“自然科学的皇后是数学,数学的皇冠是数论,‘哥德巴赫猜想’则是皇冠上的明珠。”自1742年提出至今,哥德巴赫猜想已困扰数学界长达三个世纪之久。在这个问题上取得最重大成果的中国数学家是陈景润。1973年,他在《中国科学》杂志上正式发表了完整论文,创造性地使用了一种新的“加权筛法”,证明了哥德巴赫猜想中的“1+2”。
费马大定理,由17世纪法国数学家皮耶·德·费马提出。姑且不论费马是否真的有完美的答案,单单这一挑战的提出就已经让数学界异彩纷呈。不同的地域,不同的肤色,为了同一个话题苦苦求索,追求真理的美让一代代数学大师焕发出无限光芒。最终,该定理在1994年被英国数学家安德鲁·怀尔斯证明。
美国密歇根州立大学一位26岁的学生迈克尔·谢弗花费两年时间,终于在2003年发现了已知最大的素数,这个素数可写成2的20996011次方减1,拥有6320430位数,而此前人类发现的最大素数仅有400多万位数。
……
古往今来,为什么有如此多数学家痴迷于看似“无用”的数学?这些理论研究动辄耗费数十年甚至一个人的一生,究竟有什么意义?
以色列历史学家赫拉利在《人类简史》里提出过一个观点:人类是唯一具有想象力的生灵。正是想象力,让人类不断地迭代自己的文明进程。在人类文明早期,生存是第一要素。天文、历法、农作物的播种与收获、物件的计数、财富的累积都需要数学的帮助,在这个过程中,数学逐步从满足简单的计数、计算这些日常生活需求,发展到对宇宙基本原理的认识。而数学家的兴趣和使命之一,就是探寻世界最基本的秩序和规律,诠释背后的原理,同时为现实世界的复杂现象找到最简单和本质的应对策略。
而这些,不正是我们研究数学的意义吗?
中国古代的数学研究成果
除了对圆周率的探索,古人对数学的研究从未停止。
十进制计数法
被马克思称为“最妙的发明之一”的十进制计数法,其实早在我国原始社会就已开始萌芽,到奴隶社会初期的商代已发展成完整的十进制系统。1899年,河南安阳发掘出大约3000多年前的殷代甲骨文,其中一片甲骨上刻着“八日辛亥允戈伐二千六百五十六人”(八日辛亥那天的战争中消灭敌方2656人),说明我国在公元前1600年就已经采用十进制计数法了,早于第二使用国印度1000多年!
测量太阳高度的重差术
近两千年前,我国古人就掌握了计算物体高度的方法,即“重差术”。他们把角尺直立在物体的水平位置上,对准要测量的物体,使物体的最高点与角尺两边上的两点连成一线,利用相似三角形对应边成比例的性质,计算物体高度。
后来古人突发奇想:那太阳有多高呢?当时的人们认为天圆地方,于是他们将这种方法应用到测量太阳高度上,但因为假设地面是平的,得出了错误的结果。不过,“重差术”这种数学方法是正确的。
创新专业术语的皇帝
如今我们学习解方程时,总会碰到“元”“次”“根”等术语,可你们知道吗,它们竟是康熙皇帝所创!康熙在拜比利时传教士南怀仁为师期间,为了解决翻译及表述上的困难,建议将未知数简洁地翻译为“元”,最高次数翻译为“次”(限整式方程),把方程左右两边相等的未知数的值翻译为“根”或“解”,这与原先所使用的烦琐词语有着天壤之别,因而流传至今。
此外,勾股定理、《周髀算经》、杨辉三角、幻方等,都是我国古代举世瞩目的数学成就,它们仿佛是数学历史长河中一颗颗璀璨的明珠,彰显着古人的智慧与孜孜不倦的探索精神。
数学和生活紧密相连
如果说利用数学理论改造世界对我们青少年来说为时过早,那么现在,我们完全可以利用学过的数学知识去了解这个世界。
江苏省盐城市尚庄小学的韩雨彤在和妈妈逛超市的过程中想到一个问题:为什么人民币只有1元、2元、5元、10元、20元、50元和100元,而没有其他面值呢?通过思考她明白了,原来只要有1元、2元、5元就能够组合出3元、4元、6元、7元、8元和9元;而只要有10元、20元、50元就能够组合出30元、40元、60元、70元、80元和90元,看来人民币中的学问还不小呢!
江苏省南通市如东县丰利镇石屏小学的陈佘瑞在寒假里帮爷爷奶奶当了一次小小“记账员”。家里要卖猪,爸爸妈妈不在家,爷爷奶奶又不识字,陈佘瑞就自告奋勇地揽下了算账的重任。第一头186斤、第二头201斤、第三头198斤……通过思考他想到了一个简便方法:由于捆绑每头猪的绳索和扁担的斤数是一样的,先称出1个绳索和1个扁担的斤数,乘以16就是所有绳索和扁担的总斤数,再用16头猪的总斤数减去绳索和扁担的总斤数,就是猪的净重。
生活中的数学小知识还有很多。例如,冬天猫睡觉时总是把身体抱成一个球形,这是因为体积一定时,表面积最小的形状是球体,猫缩成球体可以减少和外界接触的面积,降低热量损失速度,保持体温;风扇的叶片都是奇数,这是因为奇数的叶片组合能比偶数的叶片组合带来更多性能上的优势,如果叶片为偶数并形成对称的排列方式,那么不但风扇自身的平衡性难以维持,而且在高速运转时容易产生更多共振,导致叶片更易断裂;等等。
你们看,日常生活中很多问题的解决都离不开数学知识呢,同学们一定要努力学好数学,用数学的眼光观察、分析和解决问题。
进入21世纪,越来越多的数学理论成果开枝散叶,很多早期被认为是“无用”的数理研究,如今已成为支撑现代科技发展的澎湃动力,为我们提供越来越多的思想动力和创造源泉。同学们,希望你们站在巨人的肩膀上继续努力,为把祖国建设得更加繁荣富强做出自己的贡献!
【E学课堂】
中国古代数学成就不胜枚举,一起来扫码了解古人在计数方面的数学智慧吧!



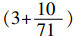 <π<
<π<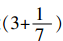 ,并计算出精确到小数点后两位的π值3.14,这是世界上首次计算出来的圆周率值。
,并计算出精确到小数点后两位的π值3.14,这是世界上首次计算出来的圆周率值。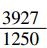 ,即3.1416,这个近似值在当时处于领先地位。
,即3.1416,这个近似值在当时处于领先地位。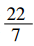 )”和“密率(
)”和“密率(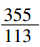 )”两个相当精确的分数来表示圆周率,闻名世界。
)”两个相当精确的分数来表示圆周率,闻名世界。