数学能力是隐性的，必须在数学活动中通过学生的行为表现出来，才能成为可观察的数学能力。数学能力在数学学习中，是以基本知识和技能、基本数学思想和基本数学活动经验来体现的。
    课程标准中关于数学能力涉及了十个核心词：数感、符号意识、空间观念、几何直观、运算能力、数据分析观念、推理能力、模型思想、应用意识和创新意识。本文中的数学能力是以这十个核心能力为基本要点，教师研究梳理出每册数学课本的每个单元想要凸显的核心能力，然后围绕这个核心能力研究制定开放性设计，组织学生试测，搜集案例并分析学生的表现，在某一个或几个核心能力点上，从学生的具体表现中提炼、抽取出能表现某一个能力水平的学生表现标准，该表现标准要能反映绝大多数学生在常规情境下的能力水平，教师可以依此标准对学生进行能力评价。
    这样教师从数学能力的角度对教材进行目标分解，最终形成小学生学习数学各单元的学习目标，并将这些学习目标转化为可评价的表现标准，将有利于分析学生的数学能力情况，进一步指导学生的学习方向和数学的教学。
    在具体实施中，教师可以研究、制定便于观察学生隐性数学能力的开放性设计，通过分析比较学生不同的解答，得出学生的数学能力的不同水平分布情况，进而达到根据学生在数学学习的能力表现，区分出学生的数学能力的五个阶段：前水平、一般水平、综合水平、结构水平和拓展水平。
    在具体研究中，笔者有以下思考。
    一、对开放性设计之开放性的思考
    有利于观察学生数学能力的开放性设计主要包含四个方面：开放性设计应有开放性问题、开放性活动、开放性任务等；开放性设计能够体现学生的思维过程，而不仅仅是结果；开放性设计让学生有充分展现的空间，不同能力的学生能有不同的表现；开放性设计要保证达到课程标准的基本要求。在研究中，教师需要在设计之初就认真研读课程标准，处理每个单元的核心能力。
    练习设计的开放性是为了让不同水平的学生都能参与，让不同水平的学生呈现不同的做法，这样就能使其隐性的数学能力显现出来，教师也可依据标准清楚认识到学生处于何种水平、数学能力的分布情况，进一步完善师生间的教学活动。
    教师编制具有开放性的题目在具体实施中有两类不同的做法。
    一类是开放性题目的答案在某种程度上是一致的，甚至是唯一的，但是学生解答的方法可以是多种多样的，不同的方法体现出不同的水平。这类似于课程标准中提出的“一题多解”。形象地来说，如图1所示，学生都需要从甲地（呈现问题）到乙地（得出结果），可以走不同的路（不同的方法），相应的道路体现相应的水平，但最后都指向一个结果。所以这样的开放性设计体现的是学生的答题过程的开放。
    另一类是开放性设计的练习不是过程性的开放，而是结果的开放。具体说就是提供一定的情境，由学生自主提出不同的问题，思考解答后得到不同的结果。如图2所示，从甲（情境）出发，学生自主提出不同的问题得到不同的结果，这个“乙”不是唯一的，是有多种结果的。

                                        图1 

                                       图2
    这两类开放性的设计，第一类需要教师编制能反映五种数学能力水平的题目，能让不同水平的学生呈现各自思维方法。往往题目本身有一定的开放性，但不能都表征学生的五种不同水平的表现，有的仅仅只能表征一种水平。所以在编制的过程中会设想学生答题方法，但是在测试中没有此种方法。第二类便于编制，但是不利于教师检测。这是因为问题很开放，不同的学生提出的问题不全相容，学生依据自己提出的个性化问题得到的答案就是多元而丰富的，甚至是教师所想不到的。
    基于这两类开放性设计，究竟是过程开放的设计有利于教学研究，还是结果开放的设计更有利于教学研究呢？
    笔者所在的小组，通过课题组的培训后，在前期实验中发现过程的开放似乎更贴近本课题研究的目的，并且从统计的角度出发，更容易判断出一个班级学生各种水平的分布情况。
例如笔者进行了六年级（上）第四单元的开放性设计题目的测试，学生情况如下：
           
    这样，分析后就会很容易发现学生学习这部分内容后已经能处于综合水平了，但是结构水平、拓展水平还未达到，说明学生还缺乏对知识之间的联系、合理建构等认知，这就为教师后续教学提供了方向。
    如果是结果开放的设计，一方面这样个性化的问题必定超出拟定的学生五种水平的表现标准之外，另一方面，提出初级问题的学生不一定就表示他的数学能力处于较低层次的水平，因为有的能力强的学生会取向选择简单的问题，所以表现出他只愿意提初步的问题。这样的开放性设计不利于教师依据标准判断。 
    由此可见，过程开放的设计更有利于教学研究，从而分析学生的数学能力分布情况。
    二、对练习开放性设计之科学性的思考
    开放性设计具备让学生把隐性的数学能力显现出来的功能，这有利于教学，同时更具科学性。教师利用这样可以检测学生每个单元目标达成情况的开放性设计以及学生的数学能力表现标准，只有在科学性的基础上才能有效指导教学。
    在研究中，笔者发现有时一个单元的核心能力很难用一道开放性设计的题目来反映五个不同的水平，所以常常需要基于一个情境下设计不同问题来反映。这样实施后，当第一个问题能测试出学生几种不同水平的时候，第二个问题因为是独立呈现给学生，学生在测试中都努力解答，这样会造成第二个问题正确率高，完成情况要好于第一个问题，随之呈现的结果就是学生较高的数学能力的百分比高于较低的数学能力百分比，有时候第二个问题还会呈现出第一个问题所表示的较低的水平，这样就不能清晰界定学生数学能力的分布情况。
    例如：笔者针对学生关于六年级（上）第一单元学习状况进行了测试。这一单元的核心能力是模型思想，笔者针对五个水平编制了两个解决实际的问题，第一个问题反映前水平、一般水平、综合水平。第二个问题反映结构水平、拓展水平。随机抽取25名学生，结果如下：
    第一题呈现的学生三种不同的水平的分布情况表
                   
    第二题呈现的学生结构水平的分布情况表
                   
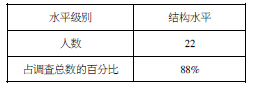
    从统计中可以看出，在抽测的学生中有72%喜欢用前水平的方式解答问题，一般水平只占24%，综合水平的有4%，但是达到结构水平的有88%。
    从实际情况来看，并不是学生都处于高水平。之所以出现上述统计的结果是研究用来表征结构水平的题目被设计成专门一题，学生都要去完成，做对的就是符合结构水平，没有做出来的就是还没达到。这种测试后统计的结果对于整个被测试群体的学习水平分布指向是由两道不同的问题测试的，结构水平和前三种水平的百分比没有可比性，这样的数据不太容易指出班级学生的整体状况，也不利于教师进一步的教学。这种状况需要进一步研究。
    三、反思
    将小学生隐性的数学能力通过具体可测的开放性设计来呈现，并运用评价的表现标准来分析，这是十分有利于数学教学的。
    基于现在的研究状况，在练习开放性设计的环节中，题目的编制特别重要。题目不仅要能准确反映单元的核心能力，更重要的是题目开放性设计要能有效区分出学生的不同数学水平。对于一线教师而言，这项工作更适合集体研究来编制，因为从开放性习题的编制到学生的表现标准都是需要抽取学生共性之处，在语言叙述上也需要适用于普遍性的原则，所以在后续操作及研究中还需重视集体研究。