浅谈《几何画板》与数学图形教学的策略
无锡市南长实验中学王宇峰 无锡市太湖格致中学黄陆珍
一、问题的提出
怎样合理利用多媒体,发挥其多样性、交互性和集成性的优点?《几何画板》以学习简单、操作方便、交互性强成为中学数学CAI(Computer Aided Instruction)首选。在不断变化的几何图形中,《几何画板》能通过度量手段发现不变的几何规律,为我们进一步研究图形提供直观的方向,促进学生对数学的理解。
二、《几何画板》在图形教学中的优点
制图速度快,精确度高 《几何画板》具有丰富的图形绘制功能,如作角、线段的垂直平分线,三角形等,精确、快速、清晰,且具有强大的“度量”和“计算”功能。
能有效地呈现元素之间关系 《几何画板》不仅能够准确地绘制几何图形,还能在运动中保持给定的几何关系,从而让学生掌握数学的本质,弥补了传统教学方式在直观感、立体感和动态感等方面的不足,便于突破传统教学的难点。
能重现几何图形的运动和变化 《几何画板》提供了平移、旋转、缩放、反射等图形变换功能,它为教学提供了一种可能——从运动的角度研究几何图形。
三、《几何画板》在教学中的使用策略
1.遵循学生认知规律
根据心理学的研究,当外部的刺激唤起主体的情感活动时,就更易成为注意的中心,从而强化理解与记忆。例如,在九年级《三角形中位线》的习题课上,笔者曾提出过这样一个问题:如图1,△ABC和△ADE是两个不全等的等腰直角三角形。现固定△ABC,而将△ADE绕点A在平面上旋转,在线段EC上是否总存在一点M,使△BMD为等腰直角三角形。
教会学生掌握知识,并非难事。困难的是让学生去发现数学结论的形成,经历一个做数学的过程,学会用数学的眼光看问题。利用《几何画板》进行探究,展示特殊情况:如图2,将△ADE绕点A顺时针旋转90°,取BD的中点F,CE的中点M,连接FM,则FM是梯形BCED的中位线,于是
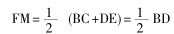 ,故△BMD为等腰直角三角形。
,故△BMD为等腰直角三角形。

图1
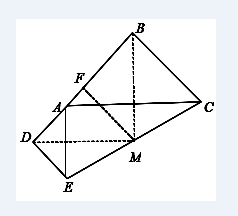
图2
对于一般情况,M是否也是CE的中点呢?利用《几何画板》进行演示,从特殊到一般,激发学生思考,符合学生的认知规律。通过对比图2和图3,找出图形中的本质属性,利于学生从题海中解脱出来,养成一个积极思考的习惯。
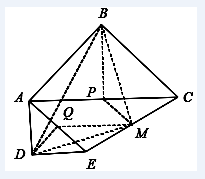
图3
2.变式训练是关键
《几何画板》可以使新知识与学生的认知结构中已有的知识建立联系,既可以避免知识庞杂而不得要领,又有利于认知结构的内化与发展,培养了学生的创造性思维。笔者在所任教班级做过这样一个测试题:如图4,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于E,AD=CE。证明:BA⊥AC。
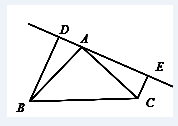
图4
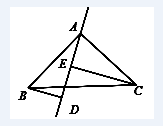
图5
班级40位学生有38位学生能找出△ABD≌△CAE。当天的家庭作业中,布置了一道变式题:如图5,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于E,AD=CE。证明:BA⊥AC。而第二日,交来的作业中能发现△ABD≌△CAE的学生只有29位。其实,两道题是一样的方法,如果在课堂上能利用一两分钟,演示一下DE绕点A旋转的过程,这样使静态的知识动态化,而动态的画面与学生的思维活动紧密相连,事半功倍。学生在这个过程中,培养了识图能力,发现了DE的位置改变了,但△ABD≌△CAE的关系没有变化,提高了学生分析问题、解决问题的能力。在此基础上,让学生学会归纳,提高数学学习的素养。
四、《几何画板》在图形教学中的建议
《几何画板》不是黑板的替代品;《几何画板》的直观不能代替学生的思考;《几何画板》得到的结论不能替代逻辑证明。
《几何画板》的广泛应用为我们的教学注入了活力,但我们也不能唯技术论,要结合教学的需要,为学生提供一个学习平台,使图形具有生命,使教学更富有活力。


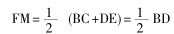 ,故△BMD为等腰直角三角形。
,故△BMD为等腰直角三角形。



